FUNGSI

Fungsi, Komposisi Fungsi, dan Invers Fungsi Matematika - Sobat hitung kali ini kita akan belajar tentang fungsi komposisi matematik SMA. Rumushitung telah merangkumkan materi tersebut semoga bisa membantu belajarnya. Let’s check this out!

Apa itu Relasi?

Dalang fungsi matematika dikenal adanya relasi. Misal sobat punya dua himpunan cowok ganteng dengan himpunan cewek jelek, kemudia sobat kaitkan anggota himpunan cowok ganteng dengan cewek jelek berdasarkan suatu hubungan tertentu maka bisa dikatakan ada relasi antera kedua himpunan tersebut. Jika himpunan cowok ganteng kita sebut himpunan A dan himpunan cewek jelek kita sebut himpunan B, maka relasi A ke B bisa dinyatakan dalam kalimat matematika

R : A → B

Contoh lain :

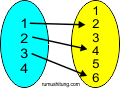
A = {1,2,3,4} dan B = [1,2,3,4,5,6} jika sobat kaitkan kedua himpunan dengan hubungan "A merupakan setengah dari B" maka relasi tersebut dapat digambarkan dalam diagram berikut

Fungsi atau Pemetaan

Apa sebenarnya yang dimakasud dengan fungsi atau pemetaan? suatu relasi dari A ke B yang memasangkan setiap anggota A dengan tepat satu anggota B disebut dengan fungsi atau pemetaan dari A ke B. Suatu fungsi umumnya dinotasikan dengan huruf ef kecil (f). Misalny f adalah fungsi yang memtakan dari A ke B, maka fungsi tersebut ditulis

f : A → B A disebut dengan daerah asal [domain]
B disebut dengan daerah kawan [codomain]

 Jikaf memetakan x ∈ A ke y ∈B maka dapat sobat hitung katakan bahwa y adalah peta dari x dan dapat ditulis f : x → y (f memetakan x ke y) atau y adalah fungsi dari x, y = f(x).

Contoh

Diagaram disamping adalah pemetaan f: A → B dengan daerah asal A = {a,b,c,d,e} daerah kawan B = {1,2,3,4,5,6} f(a) = 1; f(b) = 2; f(c) = 3; f(d) = 4; f(e) = 5, sehingga didapat range (daerah hasil) H = {1,2,3,4,5}

 fungsi yang memetakan daerah asal ke daerah kawan bermacam-macam sobat, bisa fungsi sederhana, linier, kuadrat, dan sebagainya.

Contoh
Misal f: R → R dengan f(x+2) = x²-x, tentukan berapa nilai f(x) dan f(1)
Kita misalkan y = x + 2, sehingga x = y-2
f(y) = (y-2)² – (y-2) = y² – 4y + 4 – y +2 = y² -5y + 6
sehingga bisa didapat f(x) = x² -5x + 6
f(1) = 1² -5(1) + 6 = 2

Komposisi Fungsi

Jika sobat hitung menggabungkan dua fungsi secara berurutan akan menghasilkan sebuah fungsi baru. Apa yang sobat lakukan tersebut disebut dengan mengkomposisikan fungsi dan hasilnya disebut komposisi fungsi. Coba sobat hitung simak ilustrasi berikut

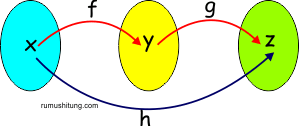
Pada diagram di atas fungsi f dikomposisikan dengan fungsi g menghasilkan fungsi h. h dinamakan fungsi komposisi dari fungsi f dan g dinotasikan h = f o g (sobat mungkin sering sebut fog atau f bundaran g). Jadi jika kira rinci

• g(y) = g(f(x))
• h(x) =  g(f(x)) atau h (x) = (g o f) (x) = g(f(x))